贝壳找房一镜到底:FM 们的原理及在贝壳搜索的实践
一、背景
在推荐系统、搜索排序、效果广告等场景中,点击率预估是十分重要的部分,CTR 算法也被誉为镶嵌在互联网技术上的明珠。在深度学习火热之前,除了简单的 LR 以外常用的算法类有:以决策树为主的 Boosting 算法;以因子分解为基础的 FM 算法。相对而言,树模型比较适合学习数值类的连续特征,而后者更适合学习 ID 类(Categorical )的稀疏特征。深度学习横空出世之后,更多的研究者把重心放在如何将 Deep Learning 运用于 CTR 任务,比较著名的有 Google 开源的 Wide and Deep 算法和 DCN 网络。通常来说,FM-based 算法更适合深度学习,深度学习需要海量的训练数据,大量稀疏的 ID 类特征为深度学习提供绝佳的土壤。
FM 的主要目的是解决稀疏特征下参数学习问题,可以实现树模型不能学习的特征交叉。本文主要涉及几个以 FM 为基础的算法。本着学习交流分享精神,本文从 FM 出发,梳理一下这些以 FM 为基础的算法。如有纰漏,敬请指出。
二、传统 FM
2.1 FM 原理
可能很多人和我一样最先接触到的并不是 FM,而是 LR、贝叶斯和决策树这些广义线性模型。在传统的线性模型中,每一维度的特征都是独立处理,当需要考虑特征与特征之间的相互作用,必须要对这些特征进行人工处理来进行交叉组合。在点击率预告的问题中通常包含着大量 ID 类特征,送入树模型中通常需要进行 onehot 编码。通过用户点击投放房屋的情况,简单介绍下 onehot 编码
| 点击 | 用户 | 小区 | 价格(万) | 面积(平方) |
|---|---|---|---|---|
| 1 | A | x | 100 | 80 |
| 0 | B | y | 60 | 50 |
| 0 | A | x | 90 | 70 |
| 1 | C | z | 200 | 100 |
对 ID 类特征进行编码之后,特征变为
| 点击 | 用户 =A | 用户 =B | 用户 =C | 小区 =x | 小区 =y | 小区 =z | 价格 | 面积 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 100 | 80 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 60 | 50 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 90 | 70 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 200 | 100 |
当数据量到达千万条以上时,将特征进行交叉组合是一个十分耗时和消耗资源的过程。并且模型在学习时会产生大量的参数,如果把 m 维的特征和 n 维的特征进行交叉将产生 mxn 个参数,加大了模型过拟合的风险。更为重要的是在特征十分稀疏的情况下,LR 和 XGB 等模型也很难学习特征之间的交叉信息,这也是因子分解机最主要的目的。
简单介绍下因子分解机的原理。我们首先考虑一个多项式模型,并对模型进行二元交叉可以得到下面的式子

其中 x 表示特征,n 代表特征维度,w 表示系数。很容易得出参数 的个数为 n(n-1)/2,当特征维度 n 很大时参数矩阵{ }几乎不可计算。思考下原因,在多项式模型中 wij 代表的是两个特征之间的系数,在特征十分稀疏(大部分 x 的值为 0)的情况下直接学习参数效率低下。FM 提出用 k 维隐向量作为来表示特征,这 k 个值都是表示特征的因子,因此被称为因子分解机,其公式如下所示

其中 v 就代表 k 维的因子。这样就将 W={ } 分解为的形式,这里就是一个的矩阵。然后我们惊奇的发现,需要训练的参数个数从 n(n-1)/2 降到 kn 。变换之后,将求解 W={wij} 的问题变成了求解。FM 算法中还有一个小技巧,利用变换对参数求解的过程进一步优化,具体的过程如下所示:
可能变换的第一步不好理解,首先我们知道 V 是一个对角阵,假设 代表的就是上三角阵元素之和(这里 A 不包括对角线元素),
代表的就是上三角阵元素之和(这里 A 不包括对角线元素), 来表示对角线元素之和,同时整个矩阵之和可表示为
来表示对角线元素之和,同时整个矩阵之和可表示为 。根据对角阵的性质我们可以得到 C = (2A + B),那么 A 就可以表示为 A=C/2 - B/2。
。根据对角阵的性质我们可以得到 C = (2A + B),那么 A 就可以表示为 A=C/2 - B/2。
在训练 FM 时,也可以和 LR 算法一样可以利用 SGD(随机梯度下降)来求解参数,各个参数的梯度如下:

在模型中, 只和 _f _有关,因此在每次迭代中,只需要计算一次就可以得到所有的梯度。原本 FM 的复杂度为
只和 _f _有关,因此在每次迭代中,只需要计算一次就可以得到所有的梯度。原本 FM 的复杂度为 ,通过上面等式的变换将其二次项化简为 v{i, f} 有关的等式,模型的复杂度降为
,通过上面等式的变换将其二次项化简为 v{i, f} 有关的等式,模型的复杂度降为 。从梯度计算的公式也可以看出,当特征值为 0 时时梯度也为 0,值为 0 的特征放到模型中训练没有意义,因此可以忽略 0 值, 这样一来 FM 就可以很快学习极其稀疏的特征。
。从梯度计算的公式也可以看出,当特征值为 0 时时梯度也为 0,值为 0 的特征放到模型中训练没有意义,因此可以忽略 0 值, 这样一来 FM 就可以很快学习极其稀疏的特征。
2.2 FFM
FFM 是 FM 的一个变种,可以说是加强版,基本的框架和 FM 一致,再其基础之上引入了域的概念。首先强推美团技术团队的《深入 FFM 原理与实践》和作者的 Slides ,看完这些就可以了解 FFM 的基本原理。FFM 的全称是 Field-aware Factorization Machine,是在因子分解机的基础之上引入了域(filed)的概念。FM 有一个很明显的缺点,它不加区分的对待每一个特征,忽略了某一类特征之间的共性。FFM 认为,由同一个 ID 类特征通过 onehot 编码产生的特征,或者其他特征变换获得的特征,应该同属于一个特殊的集合域,不同的特征和同一个域关联时需要使用不同的隐向量。假如我们一个有 d 个特征和 f 个域,那么每个特征需要用 f 个隐变量表示,也就是一共有 d x f 个隐向量。从 FFM 的公式也可以看出,

同样是上面用户点击房子的例子,在 FFM 中特征可以表示为
| Field name | Field index | Feature name | Feature index |
|---|---|---|---|
| 用户 | 1 | A | 1 |
| B | 2 | ||
| C | 3 | ||
| 小区 | 2 | x | 4 |
| y | 5 | ||
| z | 6 | ||
| 价格 | 3 | price | 7 |
| 面积 | area | 8 |
仿造 libSVM 的格式,FFM 的作者设计了 libFFM 的数据格式,如下所示
label field1: feature1: value1 field2:feature2:value2
经过简单的归一化和零值处理之后,上面的例子可以表示为

进一步的原理不再介绍,和 FM 大同小异,相对于 FM 而言,FFM 的设计更为复杂与合理。简单的来说,FM 是两个特征之间的直接交叉,FFM 更近一步特征是和域进行交叉。当只有一个域的时候,FFM 等价于 FM,也就是说其实 FM 是 FFM 把特征都归为一个域的特例。FFM 的基本原理就不在赘述,有兴趣的可以好好看看上面推荐的两个链接。
下面分享下使用 FFM 的一些注意事项:
- 归一化、归一化、归一化(重要的事情说三遍!!!),包括样本归一化和特征归一化;
- 特征编号,libffm 特征的格式为 field:index:value,有些封装好的模型包 field 编号从 0 开始,有些从 1 开始;
- 每一列的特征编号尽量不要重叠,libffm 中不允许重叠;
- 可以省略 value 为 0 的项,零值特征对模型训练没有任何贡献;
- 推荐使用 xLearn,速度十分的快。
2.3 开源工具
目前有很多开源的因子分解机工具包,主要有 libfm,libffm,xLearn 和 tffm。
| 工具包 | 语言 | GitHub | 特性 |
|---|---|---|---|
| libfm | C++ | https://github.com/srendle/libfm | 最早的 FM 工具包,由算法的提出者编写 |
| libffm | C++ | https://github.com/ycjuan/libffm | FFM 提出者编写的工具包 |
| xLearn | C++ | https://github.com/aksnzhy/xlearn | 性能强,易扩展 |
| tffm | Python | https://github.com/geffy/tffm | 基于 Tensorflow 实现 |
xLearn 是一个十分有用的机器学习工具包,由北京大学信息科学技术学院开源。目前 xLearn 已经集成了三种经典的算法,包括 LR,FM 和 FFM,适用于广告点击率预测、推荐系统等多种场景。相比与其他工具包,它的优势在于性能好和简单易用。作者在单台 MacBook 上测试,xLearn 性能远远超过其他工具包,同时提供 out-of-core 计算,利用外存计算可以在单机处理 1TB 数据,并且支持分布式训练。另外一个令人欣喜的是,xLearn 提供了 python 接口,调用起来十分的方便。

接下来将用我司(贝壳找房)真实小批量原始数据集上进行实验,其中 field 数量为 34,特征维度为 1407926。以下试验均省略掉构建 FM 和 FFM 特定的训练文件的过程,只对比训练的时间和效果。xLearn 的代码比较简单,同时也支持 CSV、libsvm、libffm 等多种格式。由于 FFM 算法只支持 libffm 格式,实验代码中均用 libffm 的格式来表示,代码如下:
1. `import xlearn as xl #载入工具包` 2. `def train_model(model_type = 'ffm', train_path = '', valid_path = ''):` 3. `#训练 lr fm ffm 中其中一个模型` 4. `if model_type == 'ffm':` 5. `model = xl.create_ffm()` 6. `elif model_type == 'fm':` 7. `model = xl.create_fm()` 8. `else:` 9. `model = xl.create_linear()` 10. `print 'This is ',model_type` 11. `model.setTrain(train_path) #导入训练集` 12. `model.setValidate(valid_path) #导入验证集` 13. `#设定超参数` 14. `param = {'task':'binary', 'lr':0.02, 'lambda':0.002, 'metric':'auc', 'epoch':100, 'k':10} #k表示隐变量的维度` 15. `model.fit(param, './model.out') #模型训练` 16. `model.setTest(valid_path) #导入验证集` 17. `model.setSigmoid() #保证输出0-1` 18. `model.predict('./model.out', './output.txt') #预测` 19. 20. `if __name__ == "__main__":` 21. `train_path = './data/ffm/tr.ffm' #训练集地址` 22. `valid_path = './data/ffm/va.ffm' #验证集和测试集使用同一个` 23. `#训练3个不同的模型` 24. `train_model('ffm', train_path, valid_path)` 25. `train_model('fm', train_path, valid_path)` 26. `train_model('lr', train_path, valid_path)`
因为没有封装好的 Python 接口,libfm 和 libffm 不能和 xLearn 一样使用 pip install 等快速安装方式。需要将它们的源码下载到本地利用命令行进行操作, 基本流程是使用 make 命令编译之后生成执行程序,再利用这些程序来训练和预测。保证超参数基本一致,libfm 的训练命令如下:
1. `./libFM -task c -train ./data/fm/tr.fm` 2. `-test ./data/fm/va.fm` 3. `-dim '1,1,10' -iter 100` 4. `-method sgd -learn_rate 0.02` 5. `-regular '0,0,0.002'` 6. `-out output`
其中,c 代表分类任务,参数 dim 表示各维度的操作,前面两个 1 分别代码加入偏置和一元交叉,10 表示二元交叉维度的大小也就是隐变量的维度,参数 regular 分别代表 L0、L1 和 L2 正则的大小。libffm 同样也需要要使用命令行来训练,需要注意的是,与前者不同 libffm 的训练和预测是两个分开的命令。
1. `./ffm-train -l 0.002 -k 10 -t 100 -r 0.02` 2. `-p ./data/ffm/va.ffm ./data/ffm/tr.ffm model` 3. `./ffm-predict ./data/ffm/va.ffm model output`
其中,参数 l 表示 L2 正则,r 表示学习率,p 后面的是验证集,这里验证集和测试集使用同一个,model 表示模型文件,output 存放预测结果。tffm 工具包的使用也比较简单,封装好了 sklearn 的接口,与之前工具包不同的是 tffm 的特征并没有使用 lib 类型的存储格式,dense 模式需要转化成矩阵存储,sparse 模式使用 scipy 的 csr_matrix 存储。简单的调用代码如下:
1. `from tffm import TFFMClassifier` 2. `from sklearn import metric` 3. `from utils import gen_data #生成样本的本地代码` 4. 5. `X_tr, y_tr = gen_data('./data/csv/train.csv')` 6. `X_te, y_te = gen_data('./data/csv/valid.csv')` 7. 8. `model = TFFMClassifier(` 9. `rank=10,` 10. `optimizer=tf.train.AdamOptimizer(learning_rate=0.002),` 11. `n_epochs=100,` 12. `batch_size=1024,` 13. `init_std=0.001,` 14. `reg=0.02, #正则项` 15. `input_type='dense',` 16. `seed=2019` 17. `)` 18. `model.fit(X_tr, y_tr, show_progress=True)` 19. `predictions = model.predict(X_te)` 20. `print 'AUC: ', metrics.roc_auc_score(y_te, predictions)` 21. `model.destroy()`
实验的结果如下:
| 算法 | AUC | logloss | 耗时 |
|---|---|---|---|
| LR-xLearn | 0.647 | 0.519 | 6.42 |
| libfm | 0.662 | 0.483 | 76.35 |
| libffm | 0.664 | 0.498 | 137.88 |
| fm-xLearn | 0.666 | 0.485 | 9.10 |
| ffm-xLearn | 0.663 | 0.492 | 34.84 |
| tffm | 0.658 | 0.497 | 220.32 |
从实验结果可以看出:
(1)xLearn 中实现的算法与 libfm 和 libffm 效果相差不大,性能分别提高了 7 倍和 4 倍;
(2)因子分解机模型相比于 LR 有提升;
(3)从该数据集来看,ffm 与 fm 的效果差异不大;
(4)基于 python 和 tensorflow 的 tffm 耗时远大于其他工具包。
根据实验结果,有一些小小的感悟。ffm 对 fm 的提升可能是有限的,模型复杂度却大大增加,真实场景中 ffm 是否能完全替代 fm 有待商榷。tffm 虽然性能不强,效果并没有太多损耗。如今各大公司都是基于深度学习去迭代模型,tffm 不需要太多的开发即可以发布到 tf-serving 上,能提高实验的效率。
三、深度 FM
3.1 Wide & Deep
机器学习的领域中有一些令人惊艳的算法,它们的出现给研究者们带来了新的思路,甚至开拓了一个流派。在 CTR 任务中,Google 于 2016 年发表的 Wide and Deep 算法将深度学习应用于 Google Play 的推荐系统中,在行业内引起了不小的轰动。严格意义上来说,W&D 算法和这篇文章主要讲的 FM-based 模型并没有关系,但是它提出来的算法框架值得我们好好研究。目前很多算法,包括后面要提到的 deepFM 和 xDeepFM 都是基于它的算法框架进行改进。
介绍框架之前,先介绍下论文中提到的两个十分关键的名词 memorization 和 generalization。简单的来说,memorization 和 generalization 是处理特征的两种方式,memorization 考虑的是如何将原始特征包含尽可能的表达出来,generalization 则是如何泛化学习到原始特征中隐藏的信息。在查阅资料时,发现一个博文很有意思,文章中有句话很好的解释了 memorization 和 generalization,原文是:The human brain is a sophisticated learning machine, forming rules by memorizing everyday events (“sparrows can fly” and “pigeons can fly”) and generalizing those learnings to apply to things we haven’t seen before (“animals with wings can fly”) 。通常来说,memorization 可以通过线性模型和特征交叉实现,generalization 则需要更多人工的特征工程。
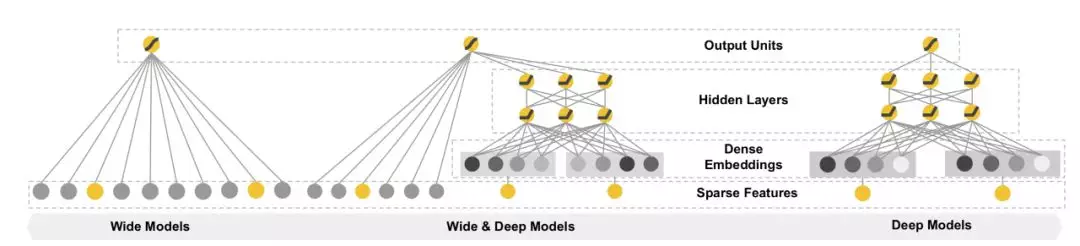
再回到 Wide & Deep 的框架就比较好理解,它可以分为两个部分,左边 Wide 部分为了 memorization,右边 Deep 部分为了 generalization。算法的思路是 LR + DNN,将 DNN 的输出和左边的 LR 连接,通过 Sigmoid 层得到输出。结合公式更加清楚,
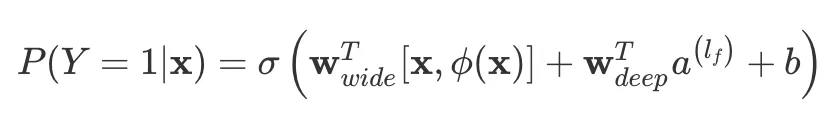
式中,是 Sigmoid 单元,是对原始特征 X 进行的交叉变换,表示 Deep 部分 通过激活函数的最终输出,W 和 b 就是常见参数矩阵和偏置。
3.2 DeepFM
计算机行业的飞速发展得益于不断创新和快速迭代。哈工大的一位学长在华为诺亚实现期间提出了 DeepFM 算法,在 Wide and Deep 的框架基础之上,将因子分解机引入到 Wide 部分。有了之前 Wide and Deep 的基础,直接来看 DeepFM 的框架图(论文的图不清楚,重画了一张图)。
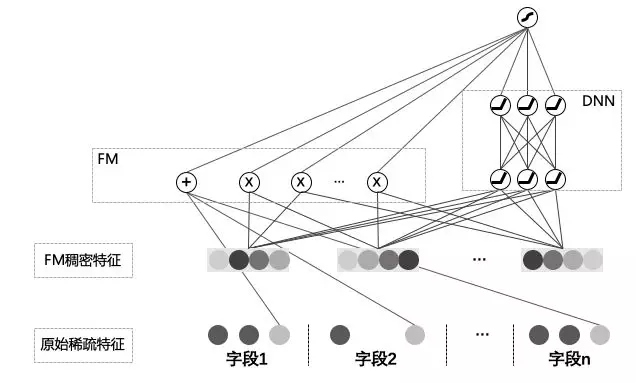
以肉眼可见 DeepFM 与 Wide and Deep 最大不同在于,DeepFM 使用了 FM 代替 LR,FM 学习交叉特征而 Deep 学习高阶特征。同属于广义线性模型,和 LR 相比 FM 的优势在于可以自动学习特征的交叉,同时又可以处理稀疏的特征,减少了使用 LR 在特征工程上的部分工作量。DeepFM 另一个重要的变化是参数共享,Wide 部分和 Deep 部分都连接在同一个 Embedding 层之后,保证了学习的一致性也提高了模型学习的效率。需要注意的是,FM 层同样用到了原始的稀疏作为输入。论文中还提到,由于 DeepFM 是端到端的训练,不需要在原始稀疏数据上做任何的人工特征工程。针对这一点,我表示怀疑,算法能学习到的始终是数学表达,脱离真实场景去对数据进行建模并不一定可行,因此针对具体业务逻辑进行人工特征工程是有必要的。
3.3 xDeepFM
在 KDD 2018 上提出一个新的模型——极深因子分解机(xDeepFM),主要是针对 DeepFM 和 DCN 进行改进。首先,xDeepFM 的算法框架仍然沿用 Wide and Deep 的框架,在 Wide 部分加入了作者称之为压缩交互网络(Compressed Interaction Network, 简称 CIN)的神经模型结构。先上整体的框架图。
xDeepFM 仍然沿用了 DeepFM 中 Embedding 共享的思路,文中没有列出的 DCN 也是如此。DCN 的改动是将 DeepFM 中的 FM Layer 替换成 Cross Network 为了学习二阶以上的交叉特征,有兴趣的可以看看原论文。受到 DCN 的启发,总结 DCN 存在的缺点,xDeepFM 的作者提出了更有效的解决办法。先介绍一下,CIN 和 其他模型不同的是特征交叉为显式的向量级(Vector-wise),而不是隐式的元素级(bit-wise)。举个例子,两个特征向量分别为 (a 1, b 1, c 1) 和 (a 2, b 2, c 2) ,f 是交叉函数,如果交叉的形式如 f(w 1 * a 1 * a 2, w 2 * b 1 * b 2, w 3 * c 1 * c 2) 为元素级的,若为 f(w*(a 1 * a 2, b 1 * b 2, c 1 * c 2)) 则称之为向量级。该作者认为,向量级的交叉特征更符合因子分解机的初衷,特征交互发生在向量级,更兼具记忆与泛化的学习能力。

下面简单介绍下 CIN,在 CIN 中每一层的神经元都是根据前一层的隐层以及原特征向量推算而来,其计算公式如下:

CIN 的计算主要有两个步骤:(1) 根据前一层隐层状态 和原始输入数据
和原始输入数据 ,计算中间结果 Z;(2) 根据中间结果,计算下一层隐层的状态。从上面的图可以看出,其实步骤(1)操作类似于 RNN 网络,而步骤(2)相当于 CNN 中池化的操作,这样看来 CIN 其实是结合了 RNN 和 CNN 的一种网络结构。
,计算中间结果 Z;(2) 根据中间结果,计算下一层隐层的状态。从上面的图可以看出,其实步骤(1)操作类似于 RNN 网络,而步骤(2)相当于 CNN 中池化的操作,这样看来 CIN 其实是结合了 RNN 和 CNN 的一种网络结构。
第一步实现的是特征维度的相互交叉,通过对原始数据的 tensor 和隐藏状态点乘操作计算出中间结果。两个 2 维从图 a 中可以看出,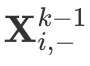 和
和 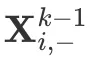 都是一个二维的矩阵,如何利用二维的矩阵相乘得到一个三维矩阵?结合下图代码来说明一下。
都是一个二维的矩阵,如何利用二维的矩阵相乘得到一个三维矩阵?结合下图代码来说明一下。
1. `for idx, layer_size in enumerate(hparams.cross_layer_sizes):` 2. `"""计算每一层的中间状态"""` 3. `#先利用将特征分隔` 4. `split_tensor = tf.split(hidden_nn_layers[-1], hparams.dim * [1], 2)` 5. `#点乘操作` 6. `dot_result_m = tf.matmul(split_tensor0, split_tensor, transpose_b=True)` 7. `#通过reshape和transpose操作变成一个三维向量` 8. `dot_result_o = tf.reshape(dot_result_m, shape=[hparams.dim, -1, field_nums[0]*field_nums[-1]])` 9. `dot_result = tf.transpose(dot_result_o, perm=[1, 0, 2])`
第二步中类似 CNN 的结构就比较简单,论文中采用了 Sum-poling 的池化方式,代码也很简单。
1. `filters = tf.get_variable(name="f_"+str(idx),` 2. `shape=[1, field_nums[-1]*field_nums[0], layer_size],` 3. `dtype=tf.float32)` 4. `curr_out = tf.nn.conv1d(dot_result, filters=filters, stride=1, padding='VALID')`
之后将串联在一起组成 CIN 层的输出。
1. `curr_out = tf.transpose(curr_out, perm=[0, 2, 1]) #转置` 2. `final_result.append(direct_connect) #有直接连接和非直接连接两种` 3. `hidden_nn_layers.append(next_hidden)` 4. `result = tf.concat(final_result, axis=1)` 5. `result = tf.reduce_sum(result, -1)` 6. 7. `hparams.logger.info("no residual network")` 8. `w_nn_output = tf.get_variable(name='w_nn_output',` 9. `shape=[final_len, 1],` 10. `dtype=tf.float32)` 11. `b_nn_output = tf.get_variable(name='b_nn_output',` 12. `shape=[1],` 13. `dtype=tf.float32,` 14. `initializer=tf.zeros_initializer())` 15. `self.layer_params.append(w_nn_output)` 16. `self.layer_params.append(b_nn_output)` 17. `exFM_out = tf.nn.xw_plus_b(result, w_nn_output, b_nn_output)`
除了 CIN 之外,剩下的 Linear 部分和 DNN 部分,xDeepFM 和 deepFM 模型保持一致。CIN 层和 DNN 层公用一个 Embedding 结果,然后将三者相加送入 Sigmoid 得到最终结果。
1. `with tf.variable_scope("exDeepFm") as scope:` 2. `with tf.variable_scope("embedding", initializer=self.initializer) as escope:` 3. `self.embedding = tf.get_variable(name='embedding_layer',` 4. `shape=[hparams.FEATURE_COUNT, hparams.dim],` 5. `dtype=tf.float32)` 6. `self.embed_params.append(self.embedding)` 7. `embed_out, embed_layer_size = self._build_embedding(hparams)` 8. `logit = self._build_linear(hparams) #Linear部分` 9. `#加上CIN部分` 10. `logit = tf.add(logit, self._build_extreme_FM(hparams, embed_out, res=False, direct=False, bias=False, reduce_D=False, f_dim=2))` 11. `#加上DNN部分` 12. `logit = tf.add(logit, self._build_dnn(hparams, embed_out, embed_layer_size))` 13. `return logit`
最后奉上之前用到小批量数据中的实验的效果对比。
| 算法 | AUC | logloss |
|---|---|---|
| Wide and Deep | 0.653 | 0.508 |
| DCN | 0.648 | 0.522 |
| DeepFM | 0.661 | 0.489 |
| xDeepFM | 0.669 | 0.481 |
可能由于数据量过少等原因,导致深度学习的模型并没有太大的优势,但是通过纵向对比,发现 xDeepFM 模型相比其他模型在 AUC 上有明显提升。
参考资料
[1]: https://tech.meituan.com/2016/03/03/deep-understanding-of-ffm-principles-and-practices.html[2]: https://www.csie.ntu.edu.tw/~r01922136/slides/ffm.pdf[3]: https://xlearn-doc-cn.readthedocs.io/en/latest/[4]: https://ke.com[5]: http://sungsoo.github.io/2017/03/27/wide-and-deep-learning-memorization-generalization-with-tensorflow.htm[6]: https://arxiv.org/pdf/1606.07792.pdf[7]: https://arxiv.org/pdf/1703.04247.pdf[8]: https://arxiv.org/pdf/1803.05170.pdf
本文作者
赵群,2019 年 1 月毕业于哈尔滨工业大学智能计算研究中心,毕业后加入贝壳语言智能与搜索部,主要从事搜索排序优化工作。




